www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Bahas Soal Matematika » Matriks ›
Jika konstanta \(k\) memenuhi persamaan \( \begin{pmatrix} k & 1 \\ 1 & 0 \end{pmatrix} \begin{pmatrix} x-1 \\ y-1 \end{pmatrix} = \begin{pmatrix} 0 \\ k \end{pmatrix} \), maka \( x + y = \cdots \)
- \( (2+k)(1+k) \)
- \( (2-k)(1+k) \)
- \( (2-k)(1-k) \)
- \( (1+k)(1-k) \)
- \( (1-k)(2+k) \)
(SPMB 2006)
Pembahasan:
Ingat bahwa untuk \( A \cdot B = C \) maka \( B = A^{-1} \cdot C \), sehingga kita peroleh berikut:
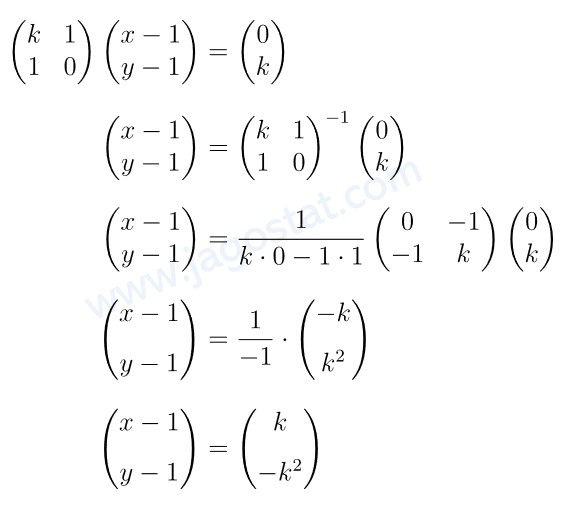
Dari kesamaan matriks di atas kita peroleh:

Jawaban B.